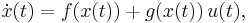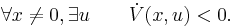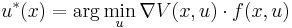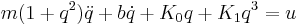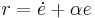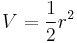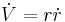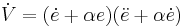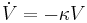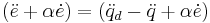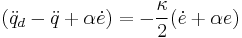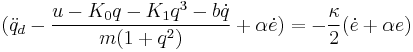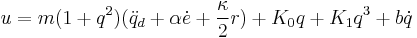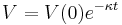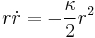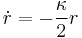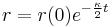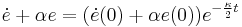Control-Lyapunov function
In control theory, a control-Lyapunov function 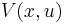 [1]is a generalization of the notion of Lyapunov function
[1]is a generalization of the notion of Lyapunov function 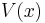 used in stability analysis. The ordinary Lyapunov function is used to test whether a dynamical system is stable (more restrictively, asymptotically stable). That is, whether the system starting in a state
used in stability analysis. The ordinary Lyapunov function is used to test whether a dynamical system is stable (more restrictively, asymptotically stable). That is, whether the system starting in a state 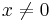 in some domain D will remain in D, or for asymptotic stability will eventually return to
in some domain D will remain in D, or for asymptotic stability will eventually return to 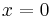 . The control-Lyapunov function is used to test whether a system is feedback stabilizable, that is whether for any state x there exists a control
. The control-Lyapunov function is used to test whether a system is feedback stabilizable, that is whether for any state x there exists a control  such that the system can be brought to the zero state by applying the control u.
such that the system can be brought to the zero state by applying the control u.
More formally, suppose we are given a dynamical system
where the state x(t) and the control u(t) are vectors.
Definition. A control-Lyapunov function is a function 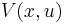 that is continuous, positive-definite (that is V(x,u) is positive except at
that is continuous, positive-definite (that is V(x,u) is positive except at 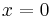 where it is zero), proper (that is
where it is zero), proper (that is 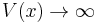 as
as 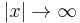 ), and such that
), and such that
The last condition is the key condition; in words it says that for each state x we can find a control u that will reduce the "energy" V. Intuitively, if in each state we can always find a way to reduce the energy, we should eventually be able to bring the energy to zero, that is to bring the system to a stop. This is made rigorous by the following result:
Artstein's theorem. The dynamical system has a differentiable control-Lyapunov function if and only if there exists a regular stabilizing feedback u(x).
It may not be easy to find a control-Lyapunov function for a given system, but if we can find one thanks to some ingenuity and luck, then the feedback stabilization problem simplifies considerably, in fact it reduces to solving a static non-linear programming problem
for each state x.
The theory and application of control-Lyapunov functions were developed by Z. Artstein and E. D. Sontag in the 1980s and 1990s.
Contents |
Example
Here is a characteristic example of applying a Lyapunov candidate function to a control problem.
Consider the non-linear system, which is a mass-spring-damper system with spring hardening and position dependent mass described by
Now given the desired state, 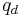 , and actual state,
, and actual state,  , with error,
, with error, 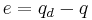 , define a function
, define a function  as
as
A Control-Lyapunov candidate is then
which is positive definite for all 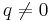 ,
, 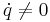 .
.
Now taking the time derivative of 
The goal is to get the time derivative to be
which is globally exponentially stable if  is globally positive definite (which it is).
is globally positive definite (which it is).
Hence we want the rightmost bracket of 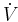 ,
,
to fulfill the requirement
which upon substitution of the dynamics, 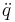 , gives
, gives
Solving for  yields the control law
yields the control law
with  and
and  , both greater than zero, as tunable parameters
, both greater than zero, as tunable parameters
This control law will guarantee global exponential stability since upon substitution into the time derivative yields, as expected
which is a linear first order differential equation which has solution
And hence the error and error rate, remembering that 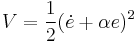 , exponentially decay to zero.
, exponentially decay to zero.
If you wish to tune a particular response from this, it is necessary to substitute back into the solution we derived for  and solve for
and solve for  . This is left as an exercise for the reader but the first few steps at the solution are:
. This is left as an exercise for the reader but the first few steps at the solution are:
which can then be solved using any linear differential equation methods.
Notes
- ^ Freeman (46)
References
- Freeman, Randy A.; Petar V. Kokotović (2008) (in English). Robust Nonlinear Control Design (illustrated, reprint ed.). Birkhäuser. pp. 257. ISBN 0817647589. http://books.google.com/books?id=_eTb4Yl0SOEC. Retrieved 2009-03-04.